Fibonacci

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0，第1项是1）。

方法一：递归

斐波那契数列公式为：\(F(n) = \begin{cases} 0, & n=0 \\ 1, & n =1,2 \\ F[n-1]+F[n-2], &n>2 \end{cases}\)，初始值\(F[0]=0,F[1]=1\) 考虑使用递归的方法。

class Solution {
public:
    int Fibonacci(int n) {
        if (n == 0 || n == 1) return n;
        return Fibonacci(n-1) + Fibonacci(n-2);
    }
};

递归算法实现简单，代码量少，但时间复杂度为\(o(2^n)\)，空间复杂度为递归栈的空间 为什么时间复杂度为\(o(2^n)\)，可以从二叉树的节点个数来考虑，递归算法可以展开为一个二叉树，所以有$n$项的递归数列，可以看成深度为\(n\)二叉树，故算法运算次数为二叉树上至多含有的节点个数\(2^n-1\)，时间复杂度为\(o(2^n)\)。

方法二：动态规划

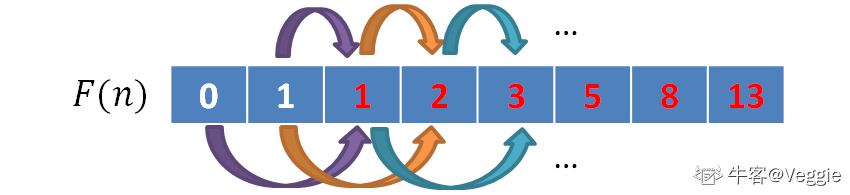
递归算法的时间复杂度高是因为存在很多重复的计算，改进办法是将计算的过程保存。动态规划是不用递归过程，直接从子树求得答案，过程是从下往上。简而言之，我们已知前两项的值，然后我们就可以用前两项的值求出第3项的值，接着求第4、第5、……，直到求出第n项的值。

int Fibonacci(int n) {
    vector<int> dp(n+1, 0);
        dp[1] = 1;
        for (int i=2; i<=n; ++i) {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
}

继续优化，例如求第五项的时候只用到第四项和第三项，因此前面的项就不需要保存，来占用内存空间。通过定义三个变量交替存储计算结果。

class Solution {
public:
    int Fibonacci(int n) {
        if (n == 0 || n == 1) return n;
        int a = 0, b = 1, c;
        for (int  i = 2; i <= n; ++i){
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }
};

时间复杂度：\(O(n)\) 空间复杂度：\(O(1)\)